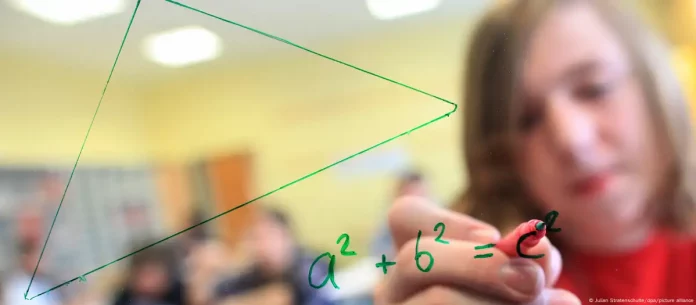Dos jóvenes científicas aficionadas a las matemáticas han conseguido lo que los expertos consideraban casi imposible: demostrar el famoso teorema de Pitágoras (a² + b² = c²) utilizando la trigonometría varias veces. Sus resultados se publicaron en la revista American Mathematical Monthly.
El quid de la cuestión: la trigonometría es una rama de la geometría, y sus fórmulas básicas se basan en la suposición de que el teorema de Pitágoras es cierto. Por tanto, existe el riesgo de que se produzca un razonamiento circular, es decir, una demostración en la que lo que se pretende demostrar es ya una presuposición.
Según la editora encargada de la publicación, los matemáticos profesionales solo han conseguido demostrarlo dos veces sin razonamiento circular. Además, hay cientos de otras pruebas del teorema milenario procedentes de otras disciplinas matemáticas, como el álgebra.
¿En qué consiste el teorema de Pitágoras?
El teorema de Pitágoras es probablemente una de las pocas fórmulas que mucha gente aún tiene en algún lugar de su mente de sus lecciones escolares. Trata de la relación entre las longitudes de los lados de un triángulo rectángulo: la suma de los cuadrados de los catetos (a y b) adyacentes al ángulo recto es igual al cuadrado de la hipotenusa (c), que está opuesta al ángulo de 90 grados. Por lo tanto, puedes calcular la longitud de cualquier lado de un triángulo rectángulo si conoces la longitud de los otros dos lados.
“El teorema de Pitágoras combina el álgebra –es decir, el cálculo con números y variables– y la geometría –es decir, el dibujo y la medición–”, explica Mario Gerwig, autor del libro El teorema de Pitágoras en 365 pruebas. Una gran colección del estadounidense Elisha Scott Loomis (1852-1940), con más de 370 pruebas, contiene exclusivamente pruebas algebraicas y geométricas.
¡Gracias por ser parte de la Experiencia de la Libertad con la comunidad de Agendamx!
¡Visita y suscríbete a nuestro canal en Youtube, dando click a la imagen!